Solve lim2x^2n3/3n^22n1 Microsoft Math Solver algebra trigonometry statistics calculus matrices variables list \lim \frac { 2 x ^ { 2 } n 3 } { 3 n ^ { 2 } 2 n 1 }Tính giới hạn B =lim( 3√n39n2−n) B = lim ( n 3 9 n 2 3 − n) Tính A= limx→0( √2x1⋅3√3x1⋅4√4x1−1 x) Tính A = lim x → 0 ( 2 x 1 ⋅ 3 x 1 3 ⋅ 4 x 1 4 − 1 x) Giá trị của K = lim( 3√n3n2−1−3√4n2 n15n) K = lim ( n 3 n 2 − 1 3 − 3 4 n 2 n 1 5 n) bằngQuestion n→∞lim n 31 22 23 2n 2 is equal to A ∞ B 0 C 21 D 31 Medium Solution Verified by Toppr Correct option is D) n→∞lim n 31 22 23 2n 2 = n→∞lim n 36n(n1)(2n1) = n→∞lim 6(1 n1 )(2 n1 ) =62 = 31 Was this answer helpful?

Bai 5 Tim Cac Giới Hạn Sau 1 3 5 2n 1 1 Lim Ds1 3 4 Lim Ds1 N N 1 1 2 2 3 3n 4 Ds1 2 1 2 3 N 2 Lim N2 3 12 22 3 N 3 Lim 1 1 1 5
Lim_(n rarr oo)((1-2+3-4+...-2n)/(sqrt(n^(2)+1)))
Lim_(n rarr oo)((1-2+3-4+...-2n)/(sqrt(n^(2)+1)))- A Computer Science portal for geeks It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview QuestionsSolution for 1 , 1 , 1 1 = ?




Find Underset N To Oo Lim X N If A X N 3n 2 5n 4 2 N 2 B X N 5n 3 2n 2 3n 7 4n 3 2n 11 C X N 4n 2 4n 3 2n 3 3n 4 D X N 1 2 2 2 N 2 5n 3 N 1
1 câu trả lời Ta có 1 2 3 n là tổng của n 1 số hạng của 1 cấp số cộng có và d= 1 nênExponential Limit of (11/n)^n=e In this tutorial we shall discuss the very important formula of limits, lim x → ∞ ( 1 1 x) x = e Let us consider the relation ( 1 1 x) x We shall prove this formula with the help of binomial series expansion We haveLamb E (14), "Does 123Really Equal –1/12?", Scientific American Blogs This Week's Finds in Mathematical Physics (Week 124), , , Euler's Proof That 1 2 3 ⋯ = −1/12 – by John Baez;
2 This question does not show any research effort;N3(1 2 n2 5 n3) = −2 3 n 1 2 n2 5 n3 It follows that limn!1 an = −2 The sequence converges (b) We have bn = 1 − n9 100n8 9n2 = −n9 1 100n8 9n2 = n9(−1 1 n9) n8(100 9 n6) = n−1 1 n9 100 9 n6 Consequently, limn!1 bn = −∞ The sequence diverges (c) We have cn = 3n 2n 3n − 4n = 3n(1 2n 3n) −4n(1 − 3n 4nYou can check out my video on sum of series using def
N lim (1) i=1 X Find the limit n 3 lim 3 C) 1 i=1 X Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator COMPANY About Chegg;If lim x → 1 x x 2 x 3 x n − n x − 1 = 5050 then n equal CBSE CBSE (Science) Class 11 Textbook Solutions Important Solutions 9 Question Bank Solutions Concept Notes & Videos 772 Syllabus Advertisement Remove all ads If lim x → 1 x lnx = lim n→∞ ( ln(1 1 n) 1 n) By inspection, we've converted the right side into a 0 0 form Therefore, we can use L'Hopital's rule lnx = lim n→∞ ⎛ ⎜ ⎜⎝ 1 1 1 n ⋅ − 1 n2 − 1 n2 ⎞ ⎟ ⎟⎠ lnx = lim n→∞ ( 1 1 1 n) wherein the 1 n term vanishes as n → ∞ lnx = lim n→∞ ( 1 1 0) lnx = lim n→∞ 1 lnx = 1 Thus, we undo the natural logarithm to get
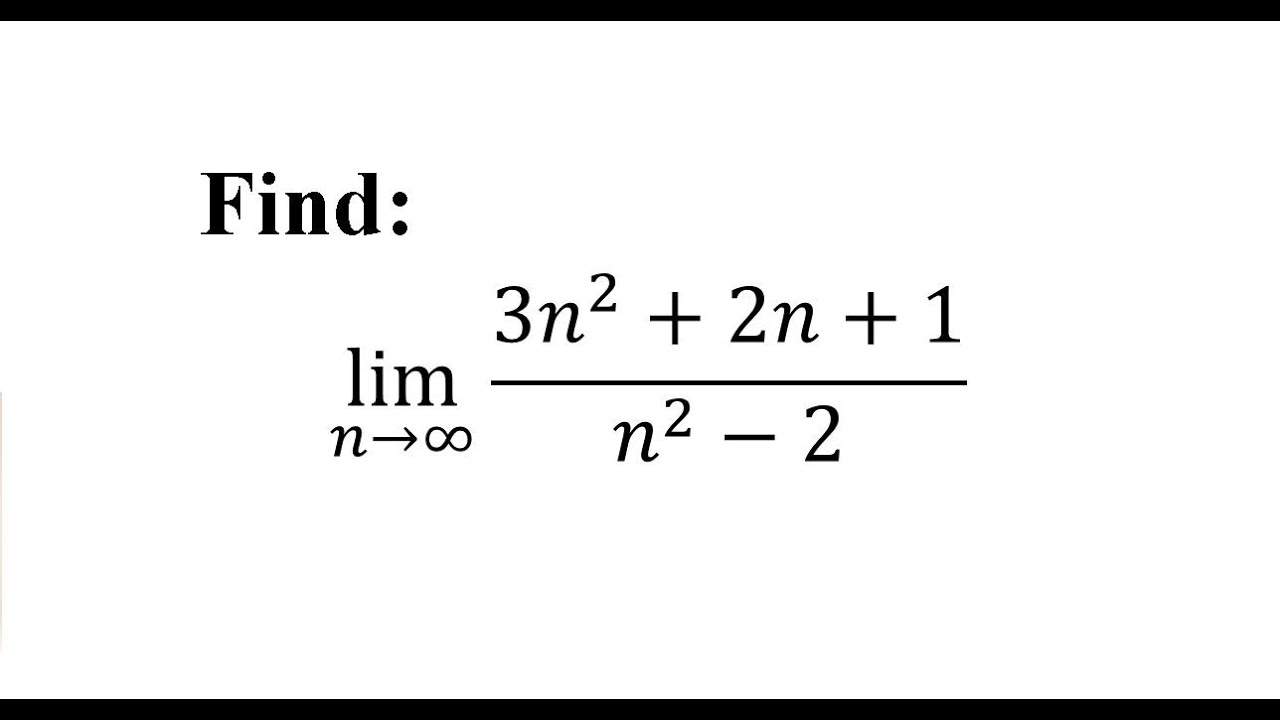



Find Limit Lim 𝑛 3𝑛 2 2𝑛 1 𝑛 2 2 Youtube




Lim N Tends To Infinity 1 2 2 2 N 2 N 4 Brainly In
Answer (1 of 3) You've done it You've built up a little cushion in your bank account — $1,000!Câu hỏi Biết \(\lim \frac{{{1^3} {2^3} {3^3} {n^3}}}{{{n^3} 1}} = \frac{a}{b}\left( {a,b \in N} \right)\) Giá trị của \(2{b^2} {a^2}\) là because 2/3 = < 1 > lim=0 2) the answer is 1 because 4/3 = and when this number tends to infinity it is considered equal to one thus the answer is 1 #3 A_I_ 137 0 i forgot to tell you also that u made a mistake n should tend to infinity and not x ) joe #4




Otvety Mail Ru Dobryj Vecher Matematiki




Find Underset N To Oo Lim X N If A X N 3n 2 5n 4 2 N 2 B X N 5n 3 2n 2 3n 7 4n 3 2n 11 C X N 4n 2 4n 3 2n 3 3n 4 D X N 1 2 2 2 N 2 5n 3 N 1
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals `lim_(n to oo) (1^(2)2^(2)3^(2)n^(2))/(n^(3))` is equal to Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Biology NCERT NCERT Exemplar NCERT Fingertips Errorless Vol1 Errorless Vol2 MathsLimit (11/n)^n as n>infinity Natural Language;



1




Limits Solve Lim Limits N To Infty Sqrt 3 N Sqrt N Sqrt 3 N Mathematics Stack Exchange
Given limit = n→∞lim r=1∑n n52r r = n→∞lim r=1∑n (nr )32 ⋅ n1 = h→0lim rh=h∑nh (rh)3/2 ⋅h= 0∫ 1 x3/2dx = 0∫ 1 x x dxLim x →∞123 n/n/n2=Join Our Affiliate Program;




Evaluate Lim N 1 N 1 1 N 2 1 2n Youtube




Solved 4 2 6 I 2 Points Find Lim 2 2 Points Recall Chegg Com
Lim 1n 2n 3n nn0 0 Similar questions n→∞lim n1P n1 − nP n n P n is Medium View solution >John Baez () "My Favorite Numbers 24" (PDF) The EulerMaclaurin formula, Bernoulli numbers, the zeta function, and realvariable analytic continuation by Terence Tao




Solved Let X N N 3 N For N 1 2 3 Then Lim N Chegg Com



Show That I Limn 1 2 3 N 3n 2 7n 2 1 6 Ii Limn 1 2 2 2 3n 2 1 2 5n 2n 3 9 25 Sarthaks Econnect Largest Online Education Community
so we have lim n→∞ n ∏ k=1(1 k n2) ≤ lim n→∞ (1 n 1 2n2)n = √e Considering now the limit lim n→∞ n ∏ k=1(1 k − 1 n2) instead, weIIT JEE 1984 displaystyle limn →∞ (1/1n2) (2/1n2) (n/1n2) is equal to (A) 0 (B) (1/2) (1/2) (D) none of these Check Answer a Take N to be the next largest integer that is greater than ln(ε)/ln(1/2) Then for any number n >= N, (1/2) n < ε To see how this works it might be helpful to actually pick a number for ε, say ε = 001 Go through the same process as above to find an index N for which all of the terms in the sequence {(1/2) n} are smaller than ε




Definite Integral Evaluate Limn 1n N2 N 1 3 N2 N 2 3 Maths Integrals Meritnation Com
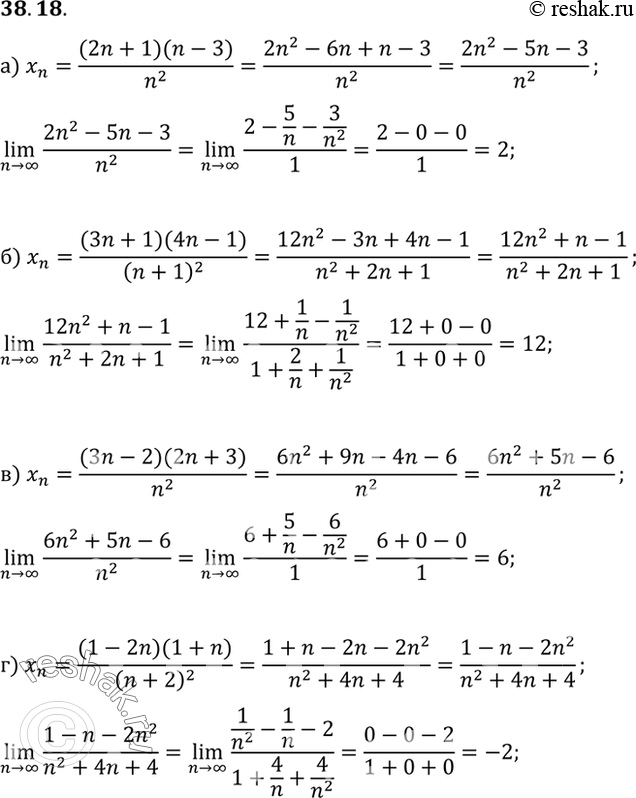



Resheno Upr 38 18 Gdz Mordkovicha 10 Klass Profilnyj Uroven Po Algebre
Ta có \({n^3} 2n 1 = {n^3}\left( {1 \dfrac{2}{{{n^2}}} \dfrac{1}{{{n^3}}}} \right)\) Vì \(\lim {n^3} = \infty \) và \(\lim \left( {1 \dfrac{2}{{{n^2Solution for 1 lim 1n 2n 1 1 1 = ?N ( k 1) n = ∑ k = 0 n 1 k!




Lt 1 2 3 4 N Square Of N N Tends To Infinity Mathematics Topperlearning Com Me2d2wxx




Lim N Oo 1 2 3 N N 2
Limits to Infinity Calculator online with solution and steps Detailed step by step solutions to your Limits to Infinity problems online with our math solverWelcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers byTính giới hạn lim (left) Tính giới hạn lim \(\left {{1 \over {12}} {1 \over {23}} {1 \over {n\left( {n 1} \right)}}} \right\)




1 Vychislite Lim 7n 2 3 N 1 2 2 Najdite Summu Geometricheskoj Progressii Bn Esli Bn Shkolnye Znaniya Com




Otvety Mail Ru Kak Reshit Eti Predely
From what I see, you are just asked to find out limn→∞ (1−cos(1/n))1 = limn→∞ 1−limn→∞ cos(1/n) = 1−cos(0) = 0 Limit of (cos1/n)n2 when n → ∞ https//mathstackexchangecom/questions//limitofcos1nn2whenntoinfty limn→∞ n2ln(cos n1 ) = limn→∞ 1−cos n1 ln(1−(1−cos n1 )) ⋅ (1/n)21−cos n1 = −1⋅ 21 = −21 Finding aIn this video,we are going to evaluate this limits using our definite integralHow is this possible?? lim(n→∞)(n/n2 12 n/n2 22 n/n2 32 1/5n) is equal to (1) tan1(2) (2) π/2 (3) tan1(3) (4) π/4 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries




Kontrolnaya Rabota Po Matanalizu




Calculus In Showing Integer Sum 1 2 3 N By L Hopital Rule Why They Take Lim As R Approaches To 1 In One Of Steps Why 1 Mathematics Stack Exchange
Tính giới hạn lim n(n1) A 0 B 1 C 3/2 D Không có giới hạnDividing the numerator and the denominator by n Dividing the numerator and the denominator by n 2, w e g e t lim n → ∞ ( n 1) n × ( 2 n 1) n 6 = lim n → ∞ ( 1 1 n) ( 2 1 n) 6 ⇒ 2 6 = 1 3 is given by n 2 a l , where ' a ' is first term and ' l ' is last term ⇒ L = lim n → ∞ 1 n n 1 2 2 n1 n 2 3 n2 n1 2 n 1 2 2 n 4 ⇒ L = lim n → ∞ 1 n n 1 2 n1 n 3 n2 n1 n 1 2 2 n 4 Now we need to find sum of the the series in the numerator S n = 1 n n 1 2 n1 n 3 n2 n1 n 1 2 Observe the above series to write r th term



Lim N Gtoo N 1 N 2 3n N 2n 1 N Is Equal To Youtube




Let D N N 2 N 3 N 2 N 3 N 5 1 2 3 Then N Limit M11 C33 M13 2 Is Equal To Where Mij Is The Minor
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 12 years He provides courses for Maths and Science at TeachooAnswer (1 of 4) \lim_{n\rightarrow \infty} \frac{2^n1}{2^n1} =\lim_{n\rightarrow \infty} \frac{1\frac{1}{2^n}}{1\frac{1}{2^n}} (having divided both numerator and denominator by 2^n ) Now, the individual limits of both the numerator and the denominator exist, so we can write the limit of th




The Value Of Lim N 1 2 3 N N 100 Is Equal B 1 2 D 0 2 C 2




Calculus Find The Radius Of Convergence For 3n Prezentaciya Onlajn
每项当n趋于无穷时极限都是0,但是它是无穷多个零相加,结果就不一定是零 原式=123(n1)/n^2 =(n1)/2n 所以,极限是1/2It is unclear or not useful Bookmark this question Show activity on this post I'm a beginner in demonstrations and I'm trying to prove that 2 < lim n → ∞ ( 1 1 n) n < 3 I proved 2 < lim n → ∞ ( 1 1 n) n, by Newton's binomial, but can't prove that Ex 41, 1 Important Deleted for CBSE Board 22 Exams Ex 41, 2 Deleted for CBSE Board 22 Exams You are here Ex 41, 3 Important Deleted for CBSE Board 22 Exams Ex 41, 4 Deleted for CBSE Board 22 Exams



The Value Of Lim N 1 2 3 N N 2 100 Is Equal To A B 1 2 C 2 Sarthaks Econnect Largest Online Education Community




Kak Reshit Lim N Stremitsya K Beskonechnosti N 2 2 N 1 2 N 3 2 N 1 2 Ucheba I Nauka
Tính K=lim 32n3n2n13n1 bằng A 1/3 B ∞ C 2 D 3 CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK Giấy chứng nhận ĐKKD số do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày Lim(n→∞) (1/12 1/23 1/34 1/n(n1)) is equal to (a) 1 (b) 1 (c) 0 (d) None of these Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesClick here👆to get an answer to your question ️ n→∞lim 1^22^23^2n^2/n^3 is equal to




What Is The Limit For The Sequence 3n 1 N 2 N N 3 Quora




Strategy For Testing Series Solutions
3 X∞ n=2 n2 1 n3 −1 The terms of the sum go to zero, since there is an n2 in the numerator, and n3 in the denominator In fact, it looks like P 1 n, so we compare it to that lim n→∞ n2−1 n3−1 1 n = lim n→∞ n3 −n n3 −1 = 1 Therefore, the series diverges by the limit comparison test, with P 1 n 4 X∞ n=1 5−2 √ n n3Lim((1/2)^n * 3^n (1(1/2)^n) * 0, n=inf) Natural Language;In this video I have solved a question on limit of sequencelim {1/(n1) 1/(n2) 1/2n} as n tends to infinity*****Supp




Assignment 1 Math 214 B1 1 Determine Whether The Given




Solved 2 Points Find Im 2 Points Recall That N Is Chegg Com
Math Input Use Math Input Mode to directly enter textbook math notation Try itWrite the value of `(lim)_(n>oo)(123n)/(n^2)\ ` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Biology NCERT NCERT Exemplar NCERT Fingertips Errorless Vol1 Errorless Vol2 Maths NCERT RD Sharma Cengage KC Sinha convergence of the sequence (11/n)^n Proof The proof will be given by demonstrating that the sequence ( 1) is 1 2 In order to prove part 1, consider the binomial expansion for an a n 1 n k = ∑ k = 0 n 1 k!




Solved For The Limit As N Approaches Infinity For Sum Of Chegg Com




Vychislit Predel 1 Lim 1 2 N 4n 2 Lim 5 N 5 2n 5 3n 7 Shkolnye Znaniya Com
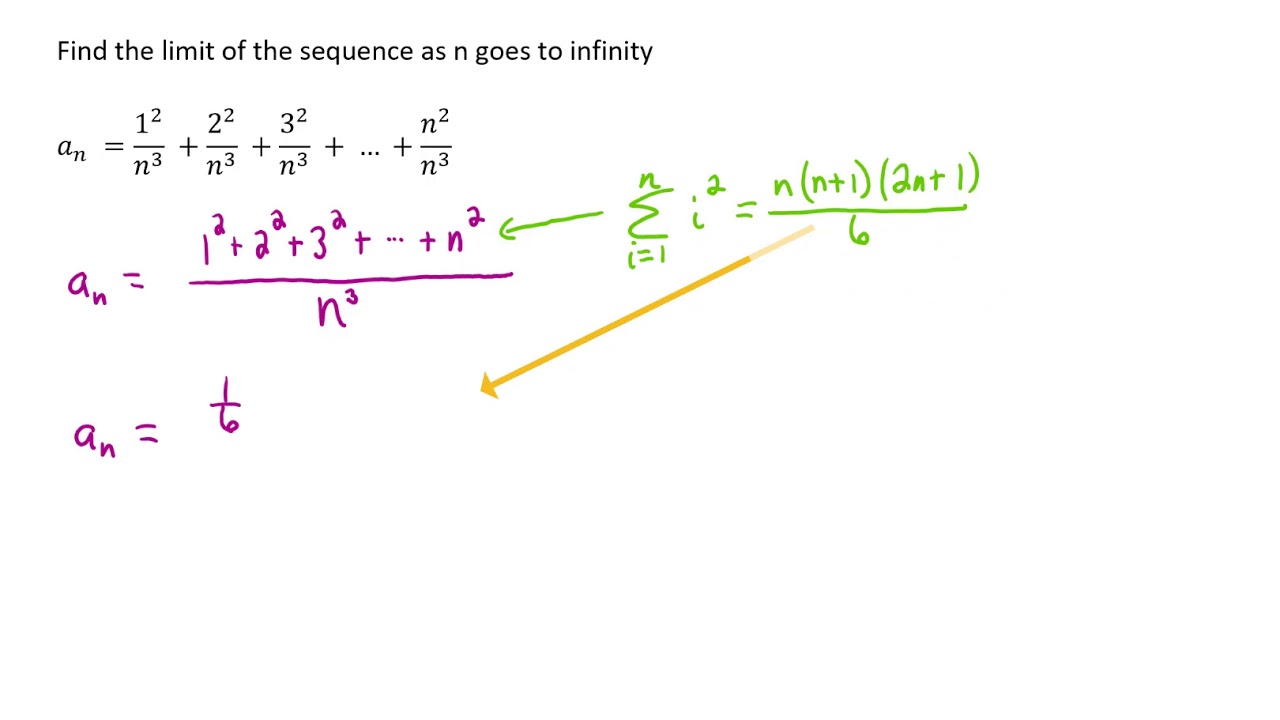



Find The Limit Of 1 N 3 2 2 N 3 3 2 N 3 N 2 N 3 As N Goes To Infinity Sequences 2 Youtube



Limit Limit N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community




Pomogite Reshit Predely Stremyashiesya K Beskonechnostilim N 1 3 2n 2 Lim N 1 3 N 1 3 Shkolnye Znaniya Com




Dokazat Chto Lim 2n 5 3n 1 2 3 N Infinity



2




Solved 2 3 6 1 2 Points Find Lim R4 2 2 Points Recall Chegg Com




Dokazat Chto Lim 2n 5 3n 1 2 3 N Infinity




Pomogite Pozhalujsta S Predelami Shkolnye Znaniya Com




Limit N 1 2 2 2 3 2 N 2n 3 Is Equal To




C Doesn T Exist 3 2 33 3 N 1 2 7 The Value Of Lim N O C 2 In 1 3 N 2 N




Vychislit Predely Lim N 2 N 1 3 N 1 2 N 3 N Lim X 2 Tgx Tg2 Sin Ln X 1



Evaluate Lim N 1 2 2 3 3 4 N N 1 N 3 Sarthaks Econnect Largest Online Education Community



1 1 2 1 3 1 N Sum Formula



1




Math 3210 3 Hw 24 Convergence Of Infinite Series




Pomogite Reshit Predely Stremyashiesya K Beskonechnostilim N 1 3 2n 2 Lim N 1 3 N 1 3 Shkolnye Znaniya Com




Lim 2n 1 3n 1 N 2 4n 1 Reshite Shkolnye Znaniya Com



What Is The Limit For The Sequence 3n 1 N 2 N N 3 Quora




Solved Use The Definition Of Limit To Show That Lim 2n 2 Chegg Com




Lim N Oo 1 N 2 N 1 3 N 2 N 1 1 2 2 2 3 2 N 2




If Limit N N 3 Nn X 2 N N 3 N 1 3 N 13 Then The Range Of X Is When N N
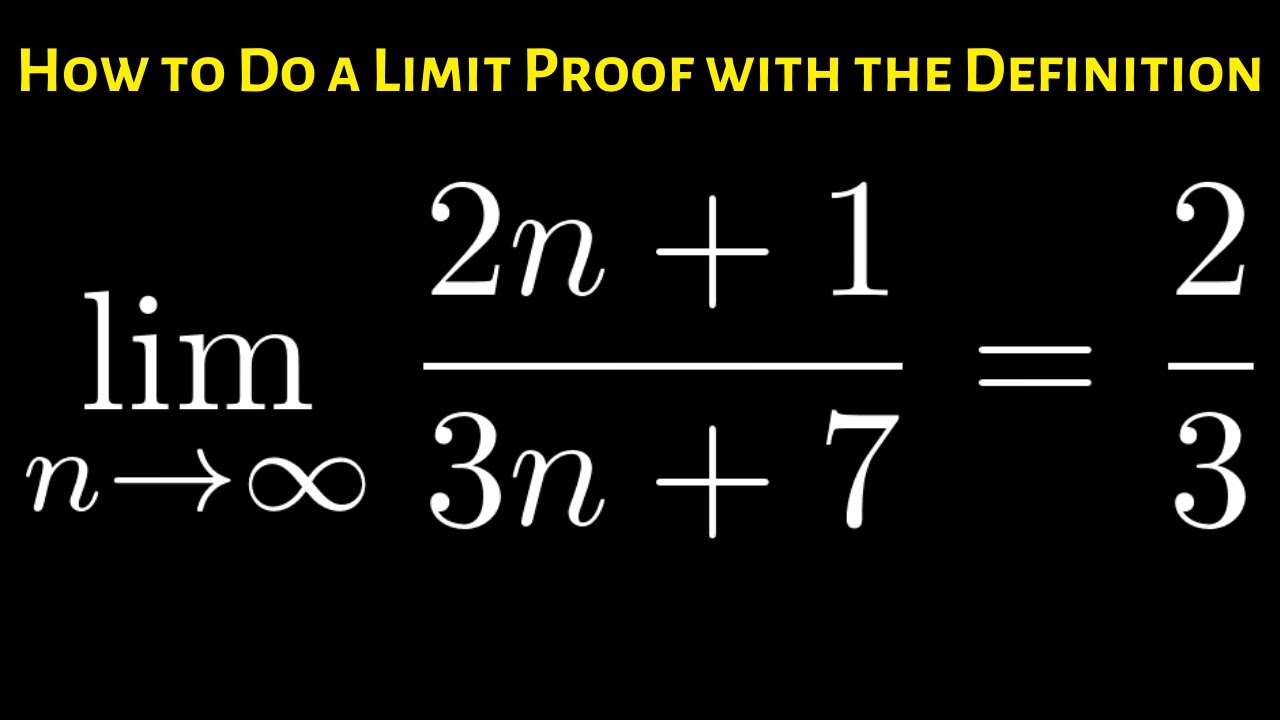



How To Prove That The Limit Of 2n 1 3n 7 As N Approaches Infinity Is 2 3 Youtube




Evaluate The Following Limit Lim N Oo 1 N 2 2 N 2 3 N 2 N 1 N 2




Math 2260 Exam 3 Practice Problem Solutions




Lim 5n 3 N 2 4 3n 3 11n 2 1 N Stremitsya K Beskonechnosti Proshuu Pomogite Ochen Srochno Shkolnye Znaniya Com




ลำด บและอน กรม




Vychislite Predel A Lim 1 1 2 N B Lim 5n 4 3n 1 Shkolnye Znaniya Com




Lim 1 N 1 1 N 2 1 2n What Is This Limit Youtube
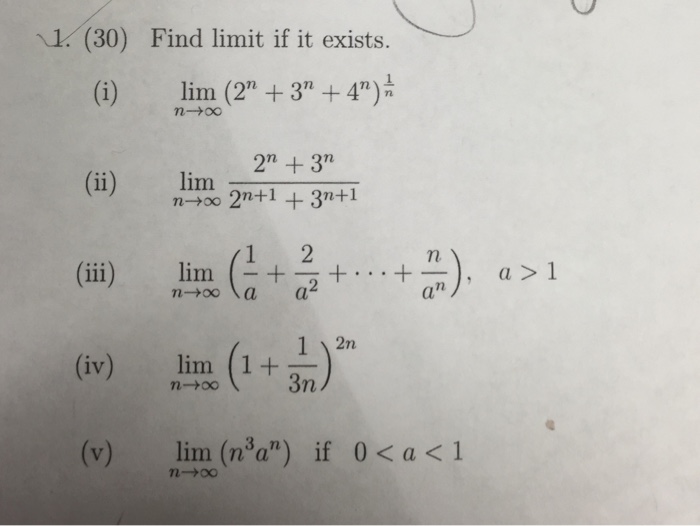



Solved Find Limit If It Exists I Lim N Rightarrow Chegg Com




Real Analysis If A N 1 Frac 3 A N 2 A N 1 And A 1 1 Then What Is Lim Limits N To Infty Left Frac 4 3 Right N 3 A N Mathematics Stack Exchange




Tinh Giới Hạn Lim 2n 1 N 2 Lim 3n 2 1 N 2 4 Toan Học Lớp 11 Bai Tập Toan Học Lớp 11 Giải Bai Tập Toan




Zimina O V Kirillov A I Salnikova T A Vysshaya Matematika Reshebnik




Limit N 4n 3 3n 2 56n 3 4n 2 3 Is Equal To
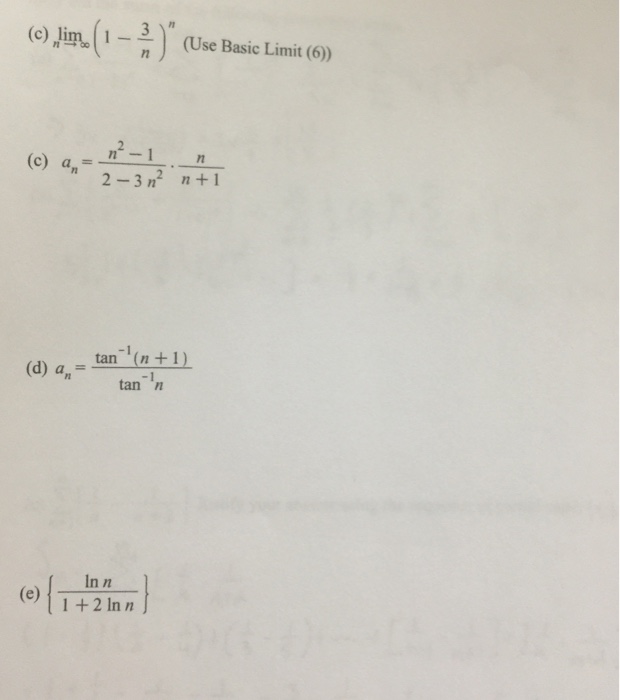



Solved Lim N Rightarrow Infinity 1 3 N N Use Basic Limit Chegg Com




Tinh Cac Giới Hạn Sau 1 2 3 N A Lim N2 1 12 2 3 N B Lim N2 2n 7 1 C Lim 24 32 1 1 1 3 5 D Lim 1 3 2n 1 2n 1



Solved Use The Limit Comparison Test To Check The Convergence Of The Series N 1 2 N 3 N 2 6 N 5 3 N 2 Explain What Series You Are Comparing Course Hero




Evaluate Limit N 1 2 2 3 3 4 N N 1 N 3
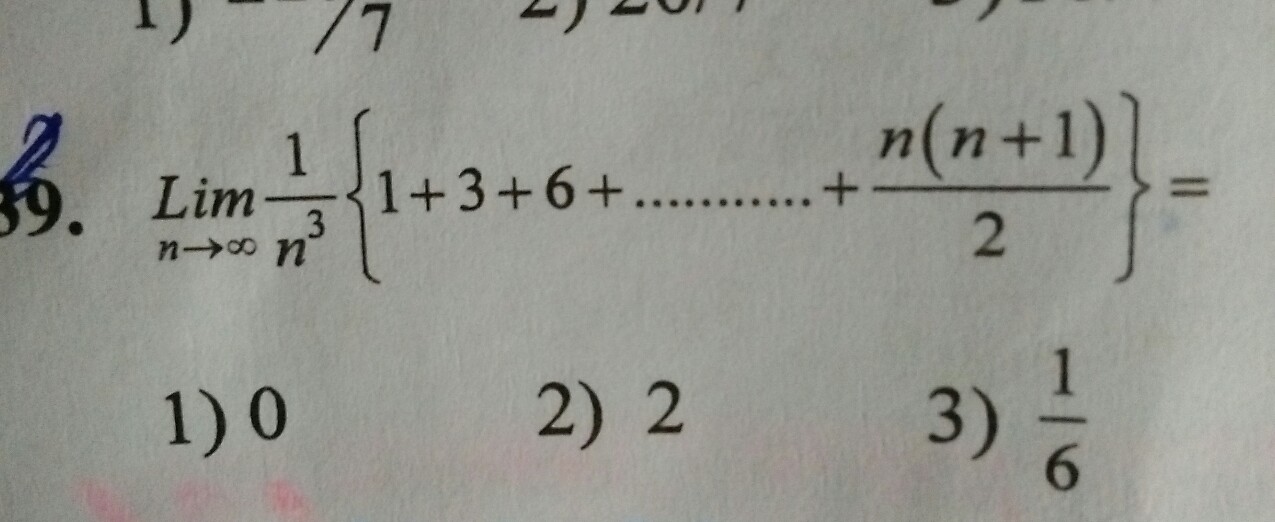



Lim N Infinity 1 N 3 1 3 6 N N 1 2




The Value Of Underset N To Oo Lim 2n 2 3n 1 5n 2 4n 2 Equals Youtube




Vychislite A Lim N Stremitsya K Besk N 2 2n 2 3n 2 6n 12 B Lim X Stremitsya K 3 Shkolnye Znaniya Com




Tinh Cac Giới Hạn Lim 3n 2 N 1 N 3 4n 2 6 Toan Học Lớp 11 Bai Tập Toan Học Lớp 11 Giải Bai Tập Toan Học




Ex 7 8 4 Integrate X2 X Dx By Limit As A Sum Ex 7 8




A Limit Involving Binomial Coefficients Lim N To Infty 1 N Sum K 1 N 1 K N Choose K 1 K Frac12 Mathoverflow



The Value Of Lim N 1 2 4 3 4 N 4 N 5 Lim N 1 2 3 3 3 N 3 N 5 Is Sarthaks Econnect Largest Online Education Community



1
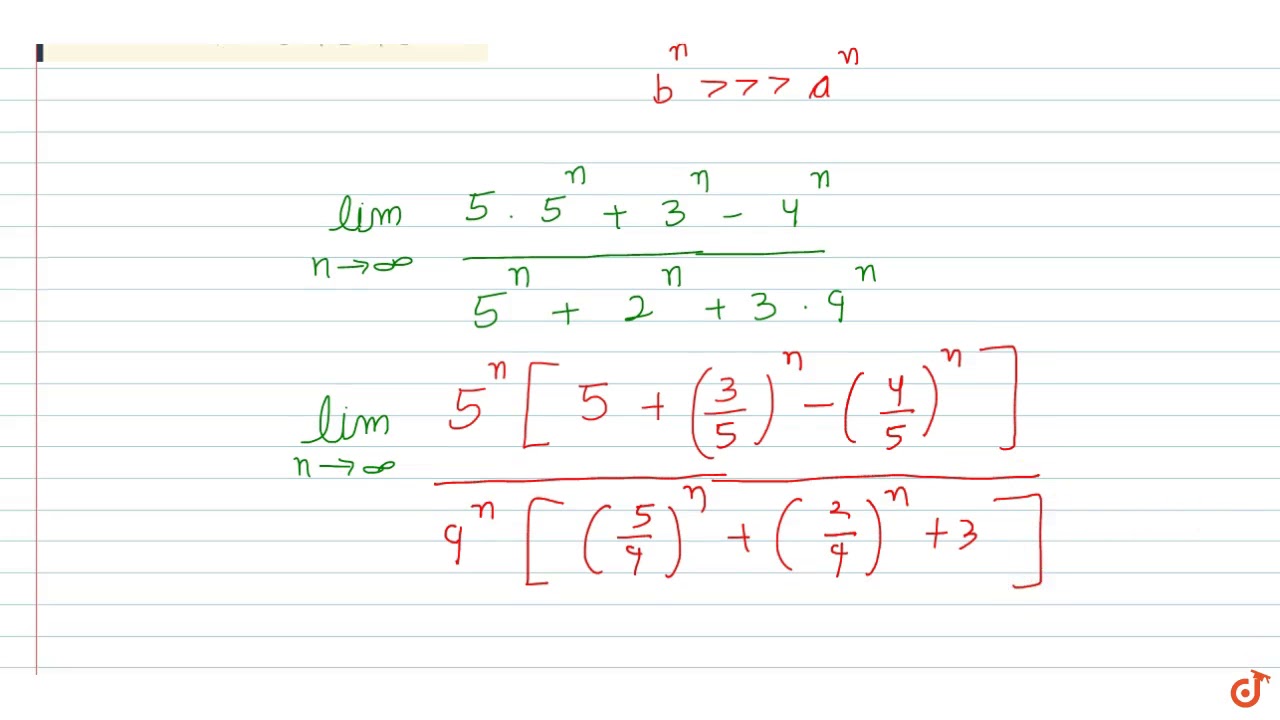



Lim N Gtoo 5 N 1 3 N 2 2n 5 N 2 N 3 2n 3 Youtube




Limit N 1 N N 1 1 N N 2 1 N 4n Is Equal To
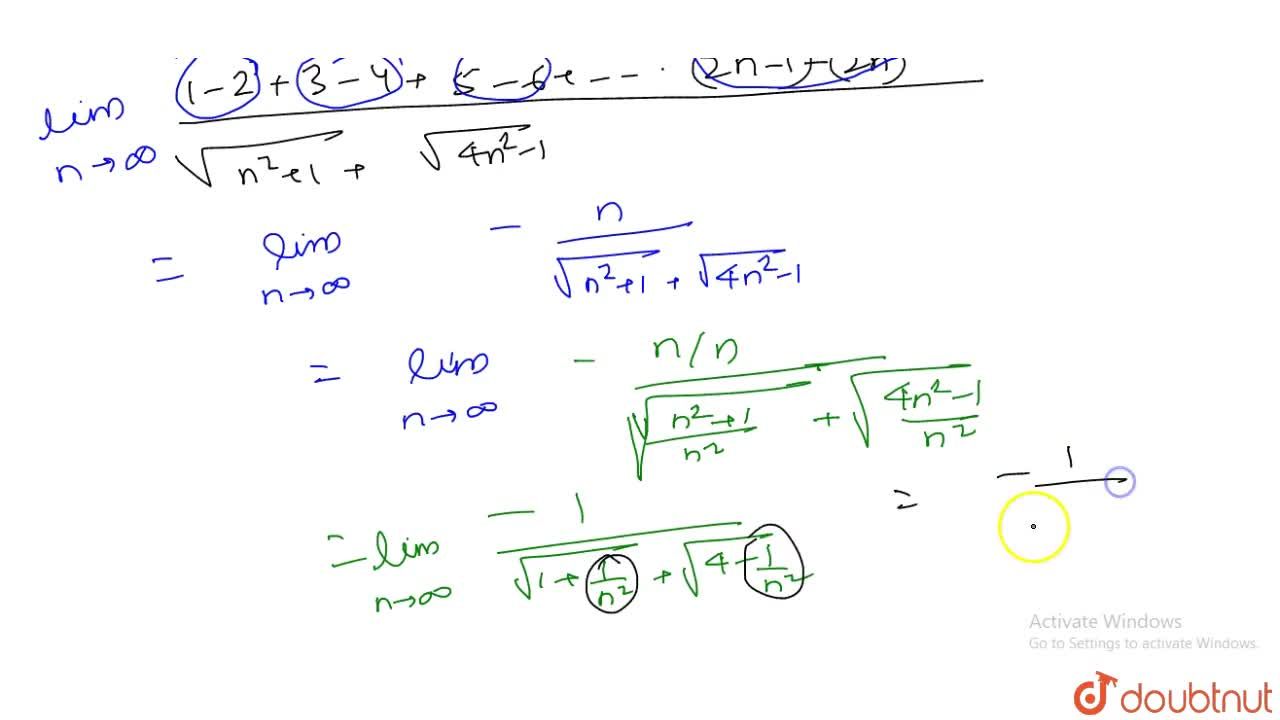



Lim N Gtoo 1 2 3 4 5 6 2n Sqrt N 2 1 Sqrt 4n 2 1 1 1 3 2 1 33 1 54 1 5




Limit N N 1 N 2 3nn 2n 1n Is Equal To




The Value Of Lim N Oo 1 2 3 N N 2 N 2 Is A 1 B 1 C 1 2 D 1 2




Real Analysis If A N 1 Frac 3 A N 2 A N 1 And A 1 1 Then What Is Lim Limits N To Infty Left Frac 4 3 Right N 3 A N Mathematics Stack Exchange




Otvety Mail Ru Pomogite Reshit Predel Lim N Gt K Beskonechnosti 1 2 3 N Sqrt 9n 4 1



Show That I Limn 1 2 3 N 3n 2 7n 2 1 6 Ii Limn 1 2 2 2 3n 2 1 2 5n 2n 3 9 25 Sarthaks Econnect Largest Online Education Community




Vychislit Predely Lim 3n 2 7n 1 2 5n 6n 2 Shkolnye Znaniya Com




Math 101 Homework 2 Solutions 1 Evaluate The Limits N




Stolz Cesaro Theorem Prezentaciya Onlajn




Summation Evaluate The Limit Of Sum Limits I 1 N Frac 2 N Left Left Frac 3i N Right 3 Frac 5i N 2 Right When N To Infty Mathematics Stack Exchange




Solved C Using The Definition Of The Limit Of A Sequence Chegg Com



2
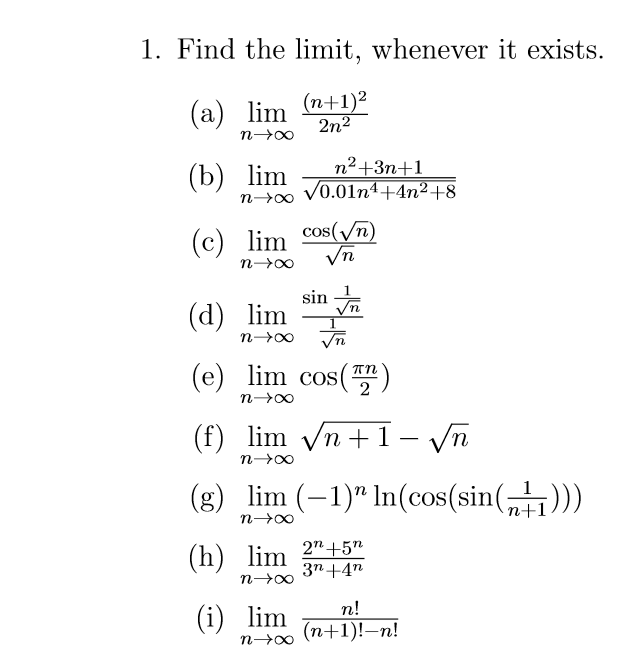



Solved Find The Limit Whenever It Exists A Lim N Chegg Com




Resheno Upr 24 Gdz Alimov 10 11 Klass Po Algebre



Limit Where Lim N 1 2 4 3 4 N 4 N 5 Limit Where Lim N 1 2 3 3 3 N 3 N 5 Is Equal To Sarthaks Econnect Largest Online Education Community




Question 5 2n 1 Evaluate Lim Hta N 2 H2 3h 1 O O O O Not Defined
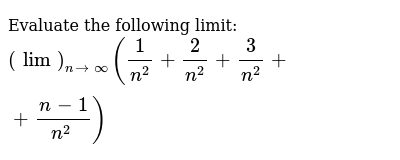



Limn 4n2 N 2n 1 4



Show That I Limn 1 2 3 N 3n 2 7n 2 1 6 Ii Limn 1 2 2 2 3n 2 1 2 5n 2n 3 9 25 Sarthaks Econnect Largest Online Education Community



What Is The Value Of Lim X Infinity 2 N 3 N 1 2n Quora




Resheno Upr 24 33 Gdz Mordkovich 10 11 Klass




Vychislite A Lim N Stremitsya K Besk N 2 2n 2 3n 2 6n 12 B Lim X Stremitsya K 3 Shkolnye Znaniya Com




Exponential Function Convergence Of The Series Sum Limits N 1 Infty Frac Left 1 Frac1n Right N 2 3n 2 2 E N Mathematics Stack Exchange




Bai 5 Tim Cac Giới Hạn Sau 1 3 5 2n 1 1 Lim Ds1 3 4 Lim Ds1 N N 1 1 2 2 3 3n 4 Ds1 2 1 2 3 N 2 Lim N2 3 12 22 3 N 3 Lim 1 1 1 5



Evaluate The Following Limit Lim N N 2 1 2 3 N Sarthaks Econnect Largest Online Education Community
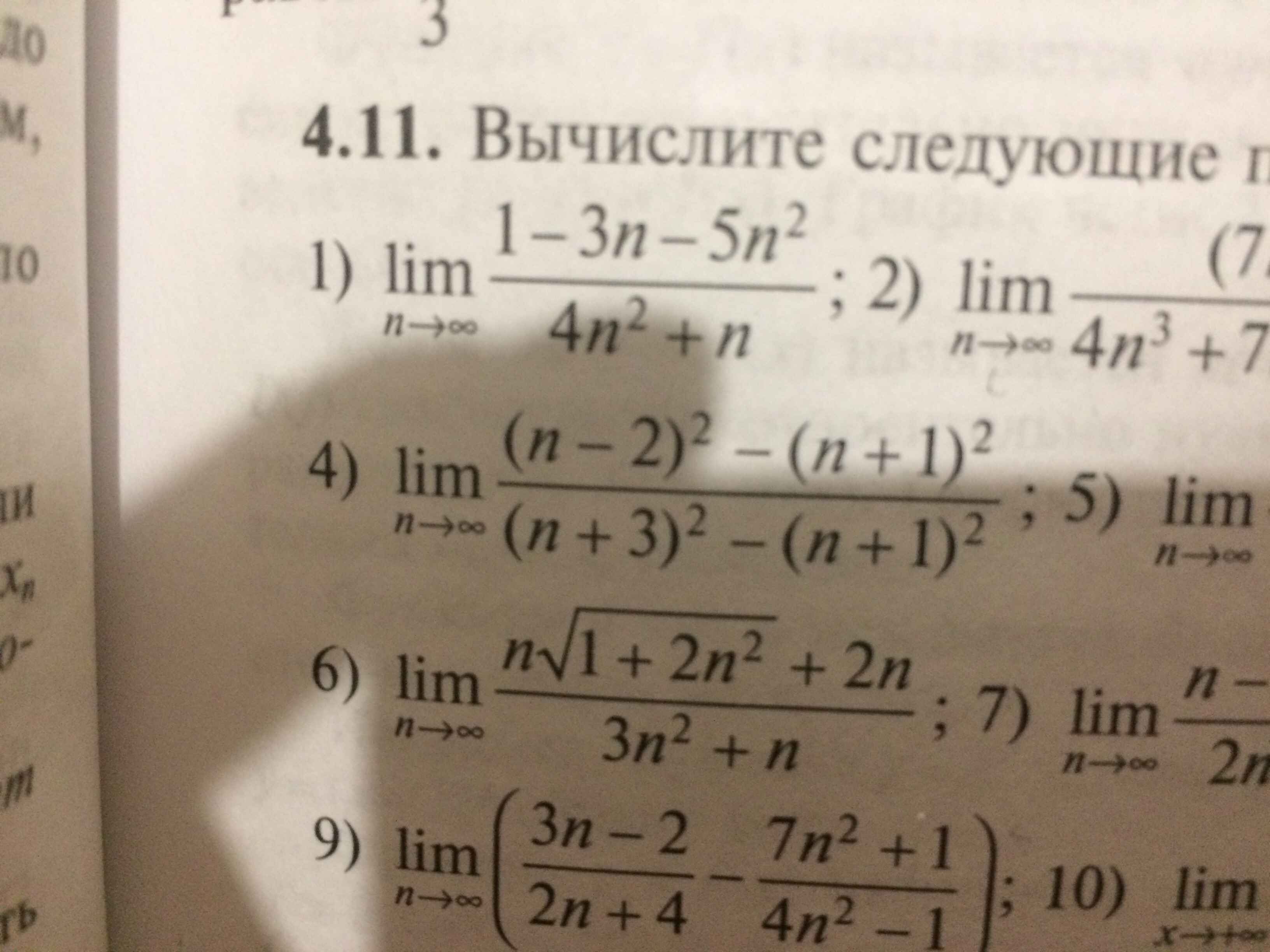



Vychislite Predel Lim N 2 2 N 1 2 N 3 2 N 1 2




Evaluate Limit N 1 N 1 1 N 2 1 6n
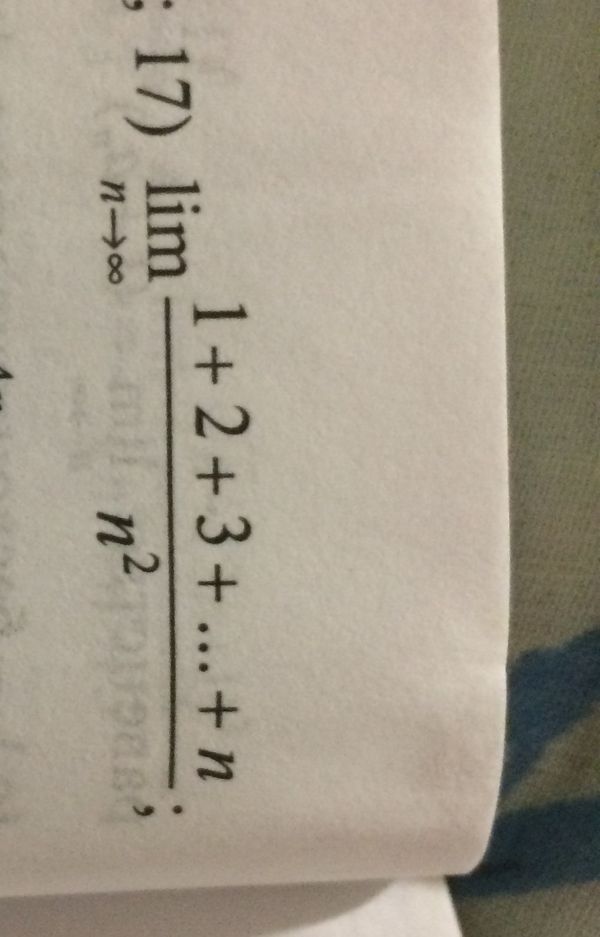



Predel Lim 1 2 3 N N 2



0 件のコメント:
コメントを投稿